1. Креслення в шкільній практиці
2. Креслення на дошці
3. Geonext
4. Приклад з геометрії
5. Динамічні креслення формату gxt
6. Креслення і розташування точок
7. Рух в геометрії
8. література

М.Д. Малих, 2012 р

Дан короткий огляд можливостей побудови креслень за допомогою пакета Geonext, розповідь ілюстрований відео-прикладами. Обговорено переваги таких креслень в порівнянні з класичними. Дистанційні з Яндекс.Відео файли доступні на Яндекс.Діск

Креслення в шкільній практиці

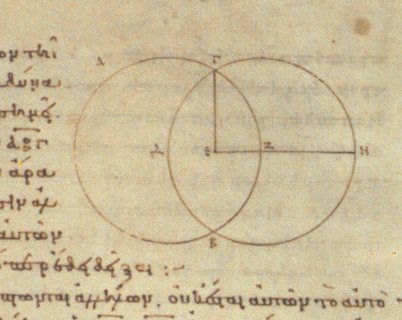
Мал. 1. Креслення на стор. 46r манускрипту D'Orville 301, Bodleian Library, Oxford.

Традиція виконання креслень в геометрії йде з часів Евкліда і не змінювалася в істотному принаймні останню тисячу років. Наприклад креслення в найстарішому з збереженому манускрипті Початки Евкліда, що зберігається зараз в Bodleian Library [ 1 ], Виглядають цілком сучасно.

За цією традицією варто багатовікова практика побудов, виконаних як від руки, так і за допомогою циркуля і лінійки. Якість виконання креслень цілком точно характеризують глибину освоєння класичної матеріалу в ту чи іншу епоху. Напр., При пізніх Каролингах в т.зв. Геометрії Боеція текст доказів не приводився, але в манускриптах були креслення з додатковими побудовами [ 2 ]. Ці креслення виконувалися від руки і часто чином, що виключає розуміння думки їх автора.

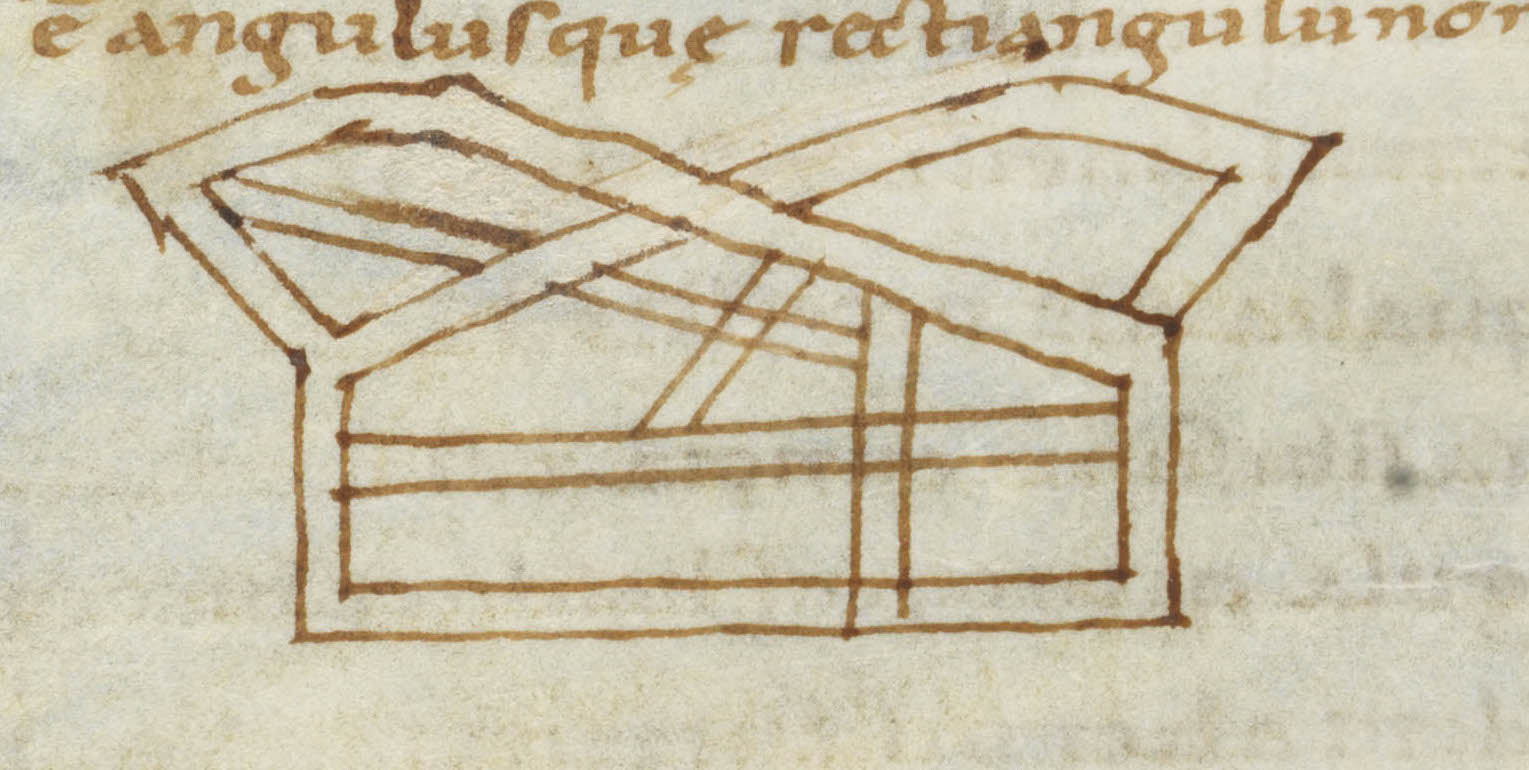
Мал. 2. Креслення до теоремі Піфагора на стор. 28 манускрипту Codex 358 (610), Einsiedeln Stiftsbibliothek [ 3 ], І сучасна ілюстрація до Евклидову доведенню теореми Піфагора.

Розвиток друкарства не привело до істотної зміни виду креслень, які виконуються в рукописах за допомогою циркуля і лінійки. Навпаки величезним технічним досягненням стало видання Ерхардом Ратдольтом в 1482 році Почав Евкліда, що відтворює не тільки текст, а й стали класичними креслення до доказів. [ 4 ]

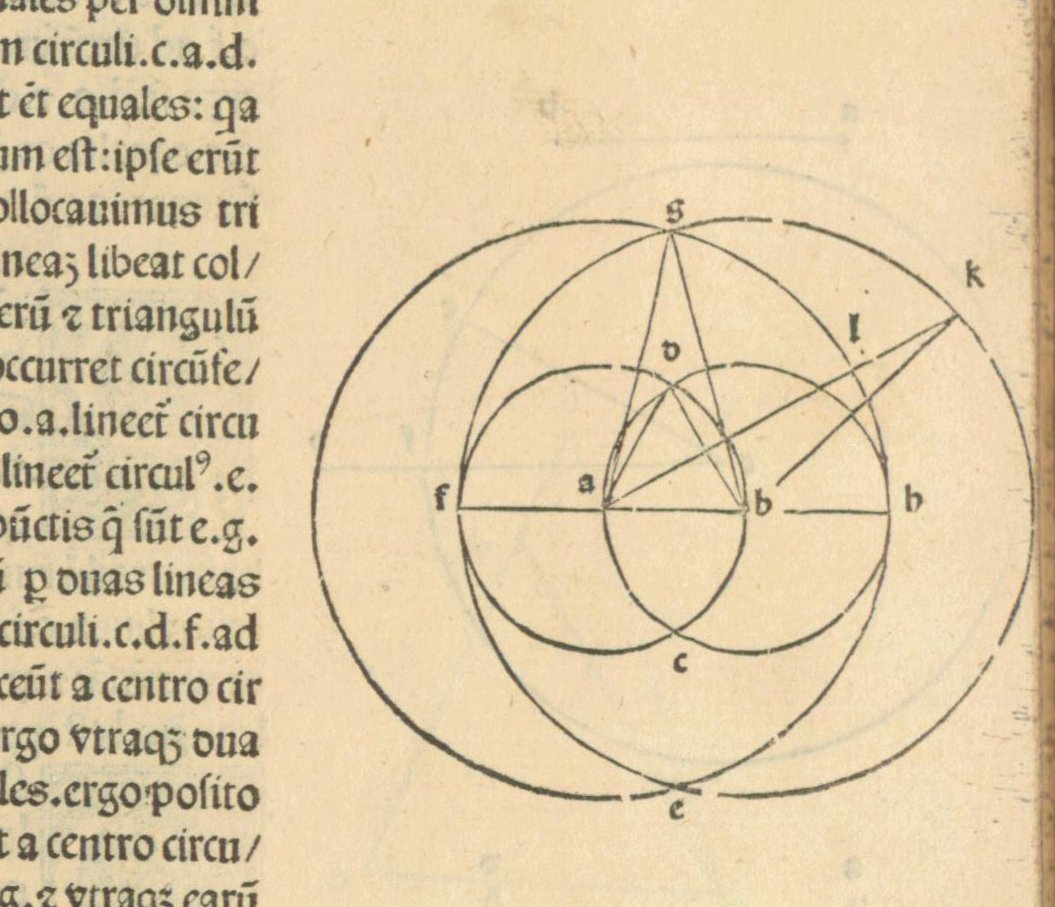
Мал. 3. Креслення з восьмої сторінки першого друкованого видання Почав Евкліда.

Нові технології, що з'явилися в книгодрукуванні в XIX столітті, були використані всерйоз лише одного разу - в виданні Почав, зробленому Олівером Бирном в 1847 році [ 5 ]. Під впливом Песталоцці Бірн хотів вигнав з геометрії для школярів буквені позначення, замінивши їх квітами. Так, напр., Замість звичних нам кутів ABC, BCA з'явилися покуття, синій кут і ін. В середині XIX століття видання книги з такою кількістю кольорових ілюстрацій стало справжнім технічним проривом, зазначеним премією на Всесвітній виставці 1851 року. Однак собівартість такої книги зупинила подальший розвиток цієї очевидно розумною з методичної точки зору ідеї.

Мал. 4. Доказ теореми Піфагора в виданні Бірна.

Більшість сучасних видань завдань з геометрії, напр., zadachi.mccme.ru , Віддають перевагу однотонним кресленнями з літерними позначеннями. Таким чином класична форма геометричного креслення не зазнала перегляду протягом декількох тисяч років.

Креслення на дошці

З давніх часів виконання крейдяних креслень на дошці є важливою частиною лекційного курсу геометрії, в т.ч. шкільних курсів геометрії і механіки і вузівського курсу аналітичної геометрії. У радянські часи вживалися спеціальні прилади для виконання побудови крейдою на дошці, однак далеко не всі вчителі і майже ніхто з вузівських лекторів не користувалися ними постійно.

З появою інтерактивних засобів навчання в середній та вищій школі і в першу чергу в зв'язку з придбанням інтерактивних дощок з'явилася вельми приваблива можливість виконувати геометричні креслення за допомогою комп'ютера. За відгуками вчителів це - один з найпоширеніших приводів для використання дощок на уроках математики.

Geonext

З початку 2000-х років на кафедрі математики і методів її викладання (Lehrstuhl für Mathematik und ihre Didaktik) університету Байройта (ФРН, Баварія) ведеться розробка системи динамічної геометрії Geonext , Яка дозволяє виконувати на інтерактивній дошці побудови майже як папері, тобто зберігаючи у школяра правильне уявлення про техніку геометричної побудови за допомогою циркуля і лінійки. Ця система повністю русифікована, орієнтована на потреби школи і протестована на німецьких школярів. Тому елементи управління надзвичайно прості і інтуїтивно зрозумілі.

Приклад з геометрії

Розглянемо простий приклад. На уроці потрібно довести теорему про те, що у будь-який трикутник можна вписати коло. Щоб не мати проблем з авторським правом, наведемо доказ по Давидову ([ 10 ], 105).

1. Розділимо два кута A і B трикутника ABC лініями OA і BO навпіл, опускаємо з точки їх припинення O перпендикуляри OL, OM і ON на сторони трикутника.

2. Прямокутні трикутники AON і AOL мають загальну гіпотенузу і з побудови кут LAO дорівнює куту NAO, отже, вони рівні, і тому ON = OL.

3. Також прямокутні трикутники OLB і MOB, що мають загальну гіпотенузу OB і рівні кути LBO і MBO, рівні, і тому LO = OM.

4. З цього випливає, що коло, описане з точки O радіусом OL, стосуватиметься всіх трьох сторін трикутника.

При виникненні труднощів можна звернутися до вельми докладного німецькому керівництву [ 6 ] Або до неофіційного керівництва Е. Адеянова [ 7 ].

Динамічні креслення формату gxt

Чорт. 1. Файл test.gxt .

Що вийшла в процесі побудови креслення можна зберегти в файл з розширенням * .gxt або зберегти як картинку (підтримуються векторний формат svg і растровий png). Креслення в форматі gxt мають ряд вельми корисних особливостей.

1. Креслення можна потягнути за будь-яку точку, при цьому бісектриса залишається биссектрисой, висота - висотою і т.д. Це дозволяє одним кресленням осягнути всі випадки. Напр., Можна швидко показати, що зміниться в кресленні, якщо один з кутів трикутника стане тупим.

2. Можна вивести список всіх побудов, що дуже корисно при вирішенні завдань на побудову. Школяр, навіть забувши записати ту чи іншу дію, завжди може підглянути кроки побудови.

3. Креслення gxt можна прямо вставляти в html-документи зі збереженням їх динамічності. Для цього в преамбулу документа слід додати

<Link rel = "stylesheet" type = "text / css" href = "http://jsxgraph.uni-bayreuth.de/distrib/jsxgraph.css" /> <script type = "text / javascript" src = "http : //jsxgraph.uni-bayreuth.de/distrib/jsxgraphcore.js "> </ script> <script type =" text / javascript "src =" http://jsxgraph.uni-bayreuth.de/distrib/GeonextReader. js "> </ script>

Потім в тілі документа, в тому місці, де потрібно вставити креслення, вставляємо рамку з ідентифікатором ris1:

<Div id = "ris1" class = "jxgbox" style = "width: 500px; height: 500px;"> </ div>

Потім вставити в неї файл test.gxt:

<Script type = "text / javascript"> var brd = JXG.JSXGraph.loadBoardFromFile ( 'ris1', 'test.gxt', 'Geonext'); </ Script>

Зрозуміло, ідентифікатор може бути будь-яким, аби він більше не зустрічався в документі. Найпростіший приклад доступний за посиланням test.html

Креслення і розташування точок

Евклід, а слідом за ним і шкільна геометрія, не завжди стежать за тим, чи всі можливі випадки взаємного положення точок розглянуті. На погано написаних фігурах точки можуть бути розставлені неможливим чином і це може бути джерелом помилок.

Доведемо, слідом за Клейном [ 8 ], За допомогою поганого креслення, що всякий трикутник є рівнобедреним слід. побудовою. Для чого в трикутнику ABC проведемо бісектрису кута A, а в середині D боку BC відновився перпендикуляр; їх перетин позначимо як O. Здається, що тут можуть представитися два випадки.

Чорт. 2. Поганий креслення для першого випадку (файл klein.gxt ).

1-ий випадок: точка O потрапила всередину трикутника. Опустимо з точки O перпендикуляри OE і OF на сторони трикутника. Оскільки OA - бісектриса, червоні прямокутні трикутники рівні, отже OE = OF. Оскільки OD серединний перпендикуляр, зелені прямокутні трикутники рівні, тому OB = OC. Але тоді рівні білі прямокутні трикутники і тому BF = EC. Значить, AB = BF + FA = CE + EA = CA, тобто вихідний трикутник рівнобедрений.

Чорт. 3. Поганий креслення для другого випадку (файл klein-2.gxt )

2-випадок: точка O потрапила поза трикутником. Знову опустимо з точки O перпендикуляри OE і OF на сторони трикутника. Оскільки OA - бісектриса, великі зелені прямокутні трикутники рівні, отже OE = OF. Оскільки OD серединний перпендикуляр, маленькі червоні прямокутні трикутники рівні, тому OB = OC. Але тоді рівні прямокутні трикутники FBO і ECO і тому BF = EC. Значить, AB = FA-FB = AE-CE = CA, тобто вихідний трикутник рівнобедрений.

Насправді, обидва розглянуті випадки неможливі. Зробивши креслення в Geonext звичайним шляхом, ми отримаємо охайний креслення.

Чорт. 4. Звичайний креслення Geonext до доказу абсурдного пропозиції (файл err.gxt ).

Звідси відразу видно, що ми упустили з розгляду випадок, коли точка O лежить поза трикутником, але один з перпендикулярів перетинає сторону трикутника. Рухаючи мишкою точки A, B і C, ми відразу бачимо, що обидва розглянуті випадки неможливі.

Креслення Geonext позбавляють шкільну практику від поганої традиції розглядати один випадок, залишаючи інші "на дім". Рухаючи точки, можна швидко перебрати всі можливі випадки взаємного розташування точок і побачити, що в доказі нічого не змінюється.

Чорт. 5. До теоремі про точку заходу висот трикутника (файл perp.gxt ). Вершини трикутника ABC можна рухати мишкою, зокрема можна вивести точку O з цього трикутника.

У цьому плані вельми показово доказ теореми про те, що висоти трикутника перетинаються в одній точці ([ 10 ], 120). Для її докази через вершини трикутника A, B і C проводять прямі, паралельний протилежними сторонам. Точки перетину цих трьох прямих утворюють новий трикутник A'B'C '. Серединні перпендикуляри цього нового трикутника збігаються з висотами трикутника ABC і вони, очевидно, перетинаються в одній точці O - центрі описаного навколо нього кола. Точка O завжди лежить всередині нового трикутника, але її положення щодо старого трикутника може бути будь-яким - в цьому легко переконається рухаючи точку C на кресленні. Наступного з паралельності прямих рівність AC = C'B = BA 'це не впливає і тому доказ не змінюється.

Рух в геометрії

У старих курсах геометрії велику увагу приділяли місцям (locus), які замітали ті чи інші точки при своєму русі.

Чорт. 6. Приклад креслення зі легкими точками (файл g3.gxt ). За точку D можна потягнути мишкою.

Напр., Нехай заданий кут ABC, а кінці відрізка DE, що має фіксовану довжину, можуть ковзати по сторонам цього кута. Яку криву описує точка G, що ділить відрізок DE у відомому відношенні? Geonext дозволяє задавати ковзаючі точки і точки, що залишають слід. Рухаючи мишкою перші, можна намалювати криві, які описують другі. На нашому рис. 6 можна тягнути за точку D і дивитися на хай точки G (цю останню теж можна пересувати уздовж DE, а також можна як завгодно змінювати кут). Спосіб створення цього креслення представлений на слід. відео.

Ще більшу користь від застосування цієї системи можуть отримати слухачі курсу проективної геометрії. У Глаголєва [ 9 ], При поясненні проектованого відповідності між прямими доводилося малювати стрілочки і словами пояснювати, куди яка точка поїде. Для прикладу на останньому кресленні задано відповідність двох прямих за трьома парам відповідних точок A, A ', B, B' і C, C '. Рухаючи точку D, можна бачити як рухається її образ D '. Змінюючи взаємне розташування точок A, B і C на прямий, можна побачити як змінюється відповідність.

Чорт. 7. Відповідність між точками двох прямих (файл proj.gxt ). Мишкою можна поміняти порядок проходження точок A, B і C на першій прямій і подивитися, в якому напрямку рухається точка D ', коли точка D рухається монотонно уздовж першої прямої.

література

1. MS D'Orville 301 . Bodleian Library, Oxford. Опис манускрипту см. В кн .: Thomas L. Heath. The Thirteen Books of Euclid's Elements, translated from the text of Heiberg, with introduction and commentary.

2. Menso Folkerts. Euclid's Elements in the middle ages . 1989.

3. Codex 358 (610) from Einsiedeln Stiftsbibliothek. Beschreibung für e-codices von P. Dr. Odo Lang OSB , Www.e-codices.unifr.ch 2009.

4. Charles Thomas-Stanford. Early editions of Euclid's Elements . London, printed for the bibliographical society. 1926.

5. Oliver Byrne. The Elements of Euclid . London, Wiliam Pickering 1847.

6. Hartmut Braun. Geonext: eine Einführung. Geonext.uni-bayreuth.de , 2011 року.

7. Е. Адеянов. Навчальний посібник за програмою GEONExT . Рига: www.skolas.lv, 2011 року.

8. Клейн Ф. Елементарна математичка з точки зору вищої. Т.2. М.-Л .: ОНТИ-ГТТІ, 1934.

9. Глаголєв Н.А. Проективна геометрія. Вища школа. 1 963.

10. Давидов А.Ю. Елементарна геометрія. М .: Лісснер і Роман, 1883.

Цей твір є по ліцензії Creative Commons «Attribution-ShareAlike» ( «Атрибуція - На тих же умовах») 3.0 Непортірованная .

Мал. 2 (правий) виконаний учасником Вікісховища під ніком Sigmanexus6 .

Конструктор uCoz