Фотограмметрії і я (від фото ... , Грец. gr á mma - запис, зображення і ... метрія ), Науково-технічна дисципліна, що займається визначенням розмірів, форми і положення об'єктів по їх зображеннях на фотознімках. Останні отримують як безпосередньо кадровими, щілинними і панорамними фотоапаратами, так і за допомогою радіолокаційних, телевізійних, інфрачервоних-теплових і лазерних систем (див. Аерометоди ). Найбільше застосування, особливо в аерофотозніманні , Мають знімки, одержувані кадровими фотоапаратами. У теорії Ф. такі знімки вважаються центральною проекцією об'єкта. Ухилення від центральної проекції, викликані дісторсией об'єктива, деформацією фотоматеріалу та ін. джерелами помилок, враховуються за даними калібрування аерофотоапарата і знімків. У Ф. використовуються поодинокі знімки і стереоскопічні їх пари. Ці стереопари дозволяють отримати стереомодель об'єкта. Розділ Ф., що вивчає об'єкти по стереопару, називається Стереофотограмметрія.

Орієнтація знімка в момент фотографування визначають три елементи внутрішнього орієнтування - фокусна відстань фотокамери f, координати x0, y0 головною точки про (рис. 1) і шість елементів зовнішнього орієнтування - координати центру проекції S - X S, Y S, Z S, поздовжній і поперечний кути нахилу знімка a і w і кут повороту c.

Між координатами точки об'єкту і її зображення на знімку існує зв'язок:

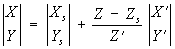, (1)

де X, Y, Z і X S, Y S, Z S - координати точок М і S в системі OXYZ; X ', Y', Z '- координати точки m в системі SXYZ, паралельної OXYZ, які обчислюють за плоским координатами х і у:

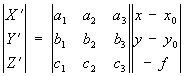. (2)

тут

a1 = cos a cos c - sin asin wsin c

a2 = - cos asin c - sin asin w cos c

a 3 = - sin acos w

b1 = cos wsin c

b2 = cos wcos c (3)

b3 = -sin w

c1 = sin acos c + cos asin wsin c,

c2 = - sin acos c + cos asin wcos c,

c3 = cos acos w

- напрямні косинуси.

Формули зв'язку між координатами точки М об'єкта (рис. 2) і координатами її зображень m1 і m2 на стереопарі P1 - P2 мають вигляд:

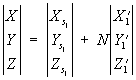, (4)

де

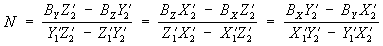, (5)

BX, BY і BZ - проекції базису В на осі координат. Якщо елементи зовнішнього орієнтування стереопари відомі, то координати точки об'єкту можна визначити за формулою (4) (метод прямої зарубки). За одиночному знімку положення точки об'єкту можна знайти в окремому випадку, коли об'єкт плоский, наприклад рівнинна місцевість (Z = const). Координати х і у точок знімків вимірюються на монокомпараторі або стереокомпараторі . Елементи внутрішнього орієнтування відомі з результатів калібрування фотоапарата, а елементи зовнішнього орієнтування можна визначити при фотографуванні об'єкта або в процесі фототріангуляцію . Якщо елементи зовнішнього орієнтування знімків невідомі, то координати точки об'єкту знаходять з використанням опорних точок (метод зворотної зарубки). Опорна точка - упізнаних на знімку контурна точка об'єкту, координати якої отримані в результаті геодезичних вимірювань або з фототріангуляцію. Застосовуючи зворотну зарубку, спочатку визначають елементи взаємного орієнтування знімків P1 - P2 (рис. 3) - a '1, c' 1, a'2, w '2, c' 2 в системі S1X'Y'Z '; вісь Х якою збігається з базисом, а вісь Z лежить в головній базисній площині S 1O1 S 2 знімка P 1. Потім обчислюють координати точок моделі в тій же системі. Нарешті, використовуючи опорні точки, переходять. від координат точок моделі до координат точок об'єкта.

Елементи взаємного орієнтування дозволяють встановити знімки в те положення відносно один одного, яке вони займали при фотографуванні об'єкта. У цьому випадку кожна пара відповідних променів, наприклад S 1m1 і S 2m2, перетинається і утворює точку (m) моделі. Сукупність променів, що належать знімку, називається зв'язкою, а центр проекції - S 1 або S 2 - вершиною зв'язки. Масштаб моделі залишається невідомим, тому що відстань S 1 S 2 між вершинами зв'язок вибирається довільно. Відповідні точки стереопари m 1 і m 2 знаходяться в одній площині, що проходить через базис S 1 S 2. Тому

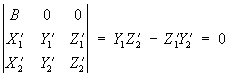(6)

Вважаючи, що наближені значення елементів взаємного орієнтування відомі, можна уявити рівняння (6) в лінійному вигляді:

a da 1 '+ b da 2' + з dw 2 '+ d dc 1' + e dc 2 '+ l = V, (7)

де da 1 ', ... e dm 2' - поправки до наближених значень невідомих, а, ..., е - приватні похідні від функції (6) по змінним a 1 ', ... c 2', l - значення функції (6), обчислене по наближеним значенням невідомих. Для визначення елементів взаємного орієнтування вимірюють координати не менше п'яти точок стереопари, а потім складають рівняння (7) і вирішують їх способом послідовних наближень. Координати точок моделі обчислюють за формулами (4), вибравши довільно довжину базису В і вважаючи X s1 = Y s1 = Z s1 = 0, BX = В, BY = BZ = 0. При цьому просторові координати точок m 1 і m 2 знаходять за формулами (2), а напрямні косинуси - по формулах (3): для знімка P 1 за елементами a 1 ', w 1' = 0, c 1 ', а для знімка P 2 по елементам a 2 ', w2', c2 '.

За координатами X 'Y' Z 'точки моделі визначають координати точки об'єкту:

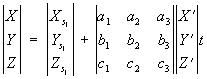, (8)

де t - знаменник масштабу моделі. Направляючі косинуси отримують за формулами (3), підставляючи замість кутів a, w і c поздовжній кут нахилу моделі x, поперечний кут нахилу моделі h і кут повороту моделі q.

Для визначення семи елементів зовнішнього орієнтування моделі - 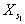, ,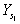, X, h, q, t - складають рівняння (8) для трьох або більше опорних точок і вирішують їх. Координати опорних точок знаходять геодезичними способами або методом фототріангуляцію. Сукупність точок об'єкта, координати яких відомі, утворює цифрову модель об'єкта, що служить для складання карти і вирішення різних інженерних завдань, наприклад для дослідження оптимальної траси дороги. Крім аналітичних методів обробки знімків, застосовуються аналогові, засновані на використанні фотограмметричних приладів - фототрансформатора , стереографія , стереопроектора та ін.

Щілинні і панорамні фотознімки, а також знімки, отримані із застосуванням радіолокаційних, телевізійних, інфрачервоних-теплових і інших знімальних систем, істотно розширюють можливості Ф., особливо при космічних дослідженнях. Але вони не мають єдиного центру проекції, і елементи зовнішнього орієнтування їх безперервно змінюються в процесі побудови зображення, що ускладнює використання таких знімків для вимірювальних цілей.

Основні переваги фотограмметричних методів робіт: велика продуктивність, тому що вимірюються об'єкти, а їх зображення; висока точність завдяки застосуванню точних апаратів і інструментів для отримання і вимірювання знімків, а також строгих способів обробки результатів вимірювань; можливість вивчення як нерухомих, так і рухомих об'єктів; повна об'єктивність результатів вимірювань; вимірювання виконуються дистанційним методом, що має особливе значення в умовах, коли об'єкти недоступні (літак, що летить або снаряд) або коли перебування в зоні об'єкта небезпечно для людини (діючий вулкан, ядерний вибух). Ф. широко застосовується для створення карт Землі, інших планет і Місяця, вимірювання геологічних елементів залягання порід і документації гірничих виробок, вивчення руху льодовиків і динаміки танення снігового покриву, визначення лесотаксационних характеристик, дослідження ерозії ґрунтів і спостереження за змінами рослинного покриву, вивчення морських хвилювань і течій і виконання підводних зйомок, вишукувань, проектування, будівництва та експлуатації інженерних споруд, спостереження за станом архітектурних ансамблів, будівель і амятніков, визначення у військовій справі координат вогневих позицій і цілей та ін.

Літ .: Бобир Н. Я., Лобанов А. Н., Федорук Г. Д., Фотограмметрія, М., 1974; Дробишев Ф. В., Основи аерофотознімання і фотограмметрії, 3 вид., М., 1973; Коншин М. Д., Аерофотограмметрія, М., 1967; Лобанов А. Н., Аерофототопографія, М., 1971; його ж, Фототопография, 3 вид., М., 1968; Дейнеко В. Ф., аерофотогеодезія, М., 1968; Соколова Н. А., Технологія великомасштабних аеротопографіческіх зйомок, М., 1973; Русинів М. М., Інженерна фотограмметрія, М., 1966; R ü ger W., Buchholtz A., Photogrammetrie, 3 Aufl, B., 1973; Manual of photogrammetry, v. 1-2, Menasha, 1966; Bonneval Н., Photogramm é trie g é né rate, t. 1-4, P., 1972; Piasecki М. B., Fotogrametria, 3 wyd., Warsz., 1973.

А. Н. Лобанов.

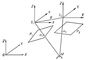
Мал. 2. до ст. Фотограмметрія.

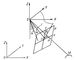
Мал. 1. до ст. Фотограмметрія.

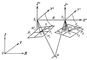
Мал. 3. до ст. Фотограмметрія.